Excess mortality in official Germany: Junk science at Destatis

You will know them by their fruits, Matthew 7:15-20

Destatis, the official German statistics agency, provides ongoing monitoring of deaths. The method for detecting excess mortality was changed in July 2021, so that since then the comparative values have been calculated from the medians of the previous years instead of the mean values as before. This change leads to a systematic error, and it is not the only one.

Destatis justifies its step with an allegedly lower susceptibility "to special developments and outliers" and adds: "The use of the median thus allows a more meaningful classification of the current death figures.

Marcel Barz, a business information scientist known as "der Erbsenzähler", who has been following the issue for some time, takes a completely different view. He uses heat maps to illustrate that Destatis detects an apparent excess mortality on the basis of medians. Therefore, he had made an official request under the Freedom of Information Act. He gives an impressive description of the reactions of the public authorities in this interview. In the same direction aims a comprehensive criticism, which the data analyst Raimund Hagemann spreads in his recent video. The elaboration impresses with argumentative force and richness of detail, and "Real Data Hero" uncovers even more inconsistencies.

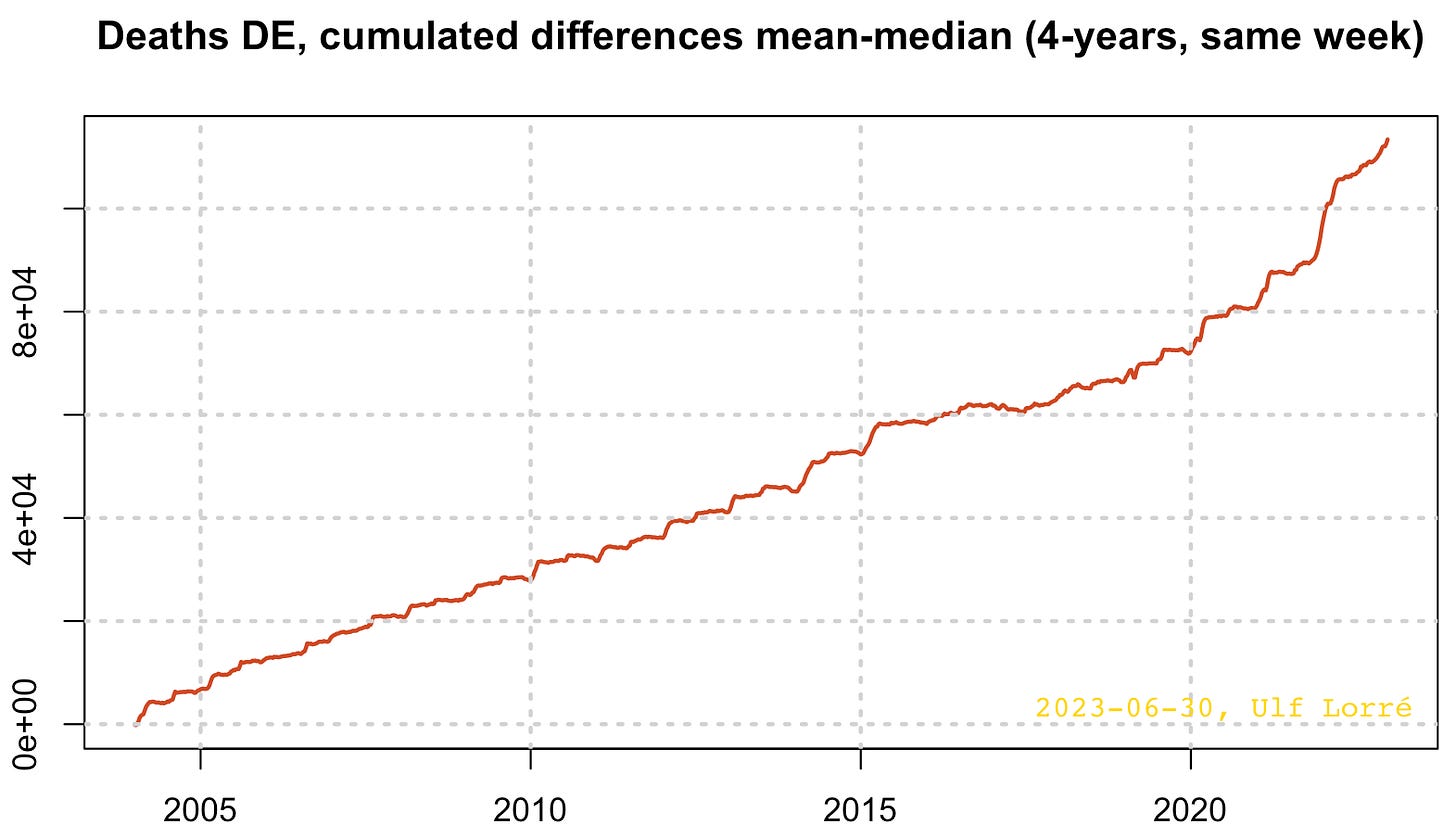
However, Barz and Hagemann do not clarify the underlying cause. I would like to add to this and, to do so, need to shed light on some mathematical basics. Let us look at the impact of the Destatis decision in a projection. Fig. 1 shows, week by week, how the summed differences of mean and median (over the last 4 years) developed from 2004 onward. In the lower part of the curve, this happened quite linearly with an increase of 4,500 p.a. on average. In recent years, the slope has increased. In the period 2020-2022, it increased to 14,000 p.a.

Fig. 1: Cumulative difference mean - median, same calendar week from 4 previous years.

Obviously, the mean values are usually higher than the medians. The reason lies in the mathematical nature of the death figures. They exhibit a skewed distribution function (Fig. 2). Skewness here means that there are higher outliers to the right than to the left, starting from the median.

Fig. 2: Frequency distribution of German death figures in the period 2016-2019.

The same property is exhibited by the figures for any other period. Fig. 3 shows this for the particularly mortality-intensive first quarters.

Fig. 3: Frequency distribution of death igures from 2013-2022, first quarter.

In the summer periods with low mortality but single heat waves, the skewness is also present, with a lower mean value (Fig. 4).

Fig. 4: Frequency distribution of death igures from 2013-2022, 25th to 35th calendar weeks.

If the median and mean differ, the question is which of the two values is preferable for comparison with later death rates.

A thought experiment answers this question. Instead of the death numbers, let us assume a series of numbers, e.g. { 1, 2, 3, 10 }, and let it repeat itself continuously. Its median 2.5 is less than the mean 4, just like the death numbers. After 4 years, this would be calculated according to the Destatis method:

------------------------------------
       Dead    deviation from median   
------------------------------------
Year 1:  1      1 - 2.5 = -1.5
Year 2:  2      2 - 2.5 = -0.5
Year 3:  3      3 - 2.5 =  0.5
Year 4: 10     10 - 2.5 =  7.5
------------------------------------
Total                      6.0

At the end of each 4-year cycle, the deviation is therefore 6, and this is what Destatis regards as excess mortality. However, it must be zero, because the same group of figures is repeated continuously. The comparison with the median therefore detects an excess mortality where none can exist.

If we compare with the mean value 4, the calculation leads to the correct result:

-----------------------------------
       Dead     deviation from mean
-----------------------------------
Year 1:  1       1 - 4 = -3
Year 2:  2       2 - 4 = -2
Year 3:  3       3 - 4 = -1
Year 4: 10      10 - 4 =  6
-----------------------------------
Total                     0

Obviously, Destatis has made its methodology worse by switching to medians, and as a result, mortality is systematically overestimated, just as Barz and Hagemann observe. But why was this decision made? A lack of technical skill is beyond question. The statistical distribution properties of mortality figures are a truism in professional circles. This is aggravated by the increasing tendency of error. The reason for this is aging. Old people show a greater seasonal variation in mortality risk and also higher outliers during above-average death waves than young people. If a population ages, these fluctuations are reflected more strongly in the total death figures. The median and mean values then drift further and further apart, and mortality is increasingly overestimated, as shown in Fig. 1.

The aging of the population has a further impact - in addition to what has already occurred. It causes the overall death rate to rise, currently by about 1% p.a. according to Destatis. Since the comparative values of a preceding 4-year period are on average 2.5 years behind, this amounts to an additional error of 2.5%. This even exceeds the median error, which was 1.7% in 2022. Taken together, Destatis thus currently operates with an overestimation of mortality of about 4.2%.

Destatis press release No. 225 reads: "May 2023 4% above the median value of previous years". We suspect what this means in reality: May was probably quite normal. As a check, consider life expectancy. In May, it deviated by only 2 per mille from the long-term expected value. If Destatis indicates a four percent excess mortality for a normal month, then this 4% is an approximate measure of the current overestimation.

All these faulty contexts and contradictions, so is to be assumed, must be fully known in the house Destatis, particularly since the criticism of Marcel Barz was brought directly to the responsible persons. It is intentional! Another interpretation is not recognizable.

What could have prompted Destatis to knowingly implement a flawed method? The timing of the decision was probably no coincidence. Every year in the middle of the year, Destatis completes the population calculation of the previous year. Consequently, in mid-2021, an assessment of the 2020 figures was on the agenda. If analyzed correctly, these would have shown that C19 did not pose an exceptional risk, because 2020 as a whole was not over-mortalized. Life expectancy even reached one of the highest values ever in Germany. Therefore, at a time when the vaccination campaign was in full swing and the most severe restrictions of fundamental rights had occurred, it should have been admitted that the sober figures had taken away the basis of the "epidemiological emergency of national significance". The political agenda, however, went in the opposite direction. In those days, hysteria continued to be stirred up, vaccination was promised as salvation, boosters were prepared, and all blame was placed on the unvaccinated. To oppose this would have required courage, and so it was apparently preferred to change the calculation mode, even if this was tantamount to a professional declassification.